In part 8, we completed the GraspCompiler class and set ourselves up to sort calculations in the order required by their dependencies. In this post, we will implement the sorting.
Interdependent Calculations
Here is an example of a set of calculations with dependencies between them:
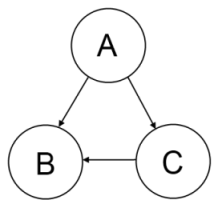
A, B, and C are output variables for calculations, and the arrows denote dependencies. They extend from the calculation which needs the data to the calculation which produces it. Analyzing this setup, we see that:
- B has no dependencies on any calculations
- C depends on B
- A depends on both B and C
In order to get correct results, we must execute these calculations such that variables are available before they are needed. In order to calculate A, we first need to calculate B and C. In order to calculate C, we must first calculate B. This means the order in which we should execute the calculations is B, then C, then A.
We can determine this order by applying a little graph theory to our calculations. This might sound imposing, but we are going to limit ourselves to very basic concepts and one well-documented algorithm. Specifically, we are going to treat the setup above as a directed acyclic graph, where each node represents a calculation and the arrows represent dependencies.
The first step is to create a way to manipulate the structure above, known as a graph. We will represent each node in the graph, then the graph itself. Once we have that data structure in place, we will use a straightforward algorithm called a topological sort to order the nodes such that calculations which produce data occur before calculations which need that data.
Nodes
Each node in a dependency graph represents a single calculation and all of its dependencies. The graph above has these nodes:
This is a more formal statement of the same observations we made before. We can create a class to represent this data structure:
internal sealed class DependencyNode
{
internal DependencyNode(
CalculationSchema calculation,
IEnumerable<CalculationSchema> dependencies)
{
Calculation = calculation;
Dependencies = dependencies.ToList().AsReadOnly();
}
internal CalculationSchema Calculation { get; private set; }
internal ReadOnlyCollection<CalculationSchema> Dependencies { get; private set; }
}
The next step is to create a set of these nodes from a set of calculations. To do this, we need to pair every calculation with every other calculation and determine if there is a dependency between each pair. Our example would produce these comparisons:
| Pairing | Dependency? |
| A –> B | Yes |
| A –> C | Yes |
| B –> A | No |
| B –> C | No |
| C –> A | No |
| C –> B | Yes |
We check both directions of each pairing because eventually we will guard against cycles. For example, if A depends on B, B depends on C, and C depends on A, there is no way to execute that set of calculations due to an infinite loop. Any graph with a cycle will result in a compilation error from Grasp.
To create the nodes, we add a method to the DependencyAnalyzer class defined in part 8:
private static IEnumerable<DependencyNode>
GetNodes(IEnumerable<CalculationSchema> calculations)
{
return
from calculation in calculations
let dependencies =
from possibleDependency in calculations
where possibleDependency != calculation
where IsDependency(calculation, possibleDependency)
select possibleDependency
select new DependencyNode(calculation, dependencies);
}
We create a LINQ query which selects all of the calculations in the sequence, then for each one does the same thing but filters out the one we are already considering. This gives us all calculation pairs in both directions. We check the original calculation against each possible dependency to determine if there is an actual dependency between them:
private static bool IsDependency(
CalculationSchema calculation,
CalculationSchema possibleDependency)
{
return calculation.Variables.Contains(possibleDependency.OutputVariable);
}
This is simply a matter of checking whether the possible dependency’s output variable is referenced by the calculation. This repeated Contains call is why we made the CalculationSchema.Variables property a HashSet<> instead of a List<>.
Graph
Once we have all the nodes in hand, we can represent the entire graph:
internal sealed class DependencyGraph
{
private readonly Dictionary<CalculationSchema, DependencyNode> _nodes;
internal DependencyGraph(IEnumerable<DependencyNode> nodes)
{
_nodes = nodes.ToDictionary(node => node.Calculation);
}
internal IEnumerable<CalculationSchema> OrderCalculations()
{
return new TopologicalSort(this).SortNodes().Select(node => node.Calculation);
}
}
We create a dictionary which associates each node with its calculation. This will be important later when we want to look up the nodes on which a node depends, as there is no direct association between nodes; the DependencyNode.Dependencies property is expressed in terms of calculations, not nodes.
The OrderCalculations method is the public API of our graph class. It creates a topological sort (discussed below), sorts the nodes in the graph, then grabs the calculation from each. The result is the ordered set of calculations, which we use to implement the DependencyAnalyzer.OrderByDependency method we left unfinished in part 8:
internal static IEnumerable<CalculationSchema>
OrderByDependency(this IEnumerable<CalculationSchema> calculations)
{
return GetGraph(calculations).OrderCalculations();
}
private static DependencyGraph
GetGraph(IEnumerable<CalculationSchema> calculations)
{
return new DependencyGraph(GetNodes(calculations));
}
This creates a graph by calling the GetNodes method we defined above, then returns the ordered set of calculations to be compiled by GraspCompiler. This set of methods is simply how we weave the data and algorithm together; the truly interesting logic is in the sorting itself.
Topological Sorting
A topological sort is a way of ordering a set of nodes such that less-dependent nodes appear first and the more-dependent nodes appear later. Applying this sort to our example would yield the calculations in the order B, C, A.
The general idea is to start from each node in the graph and walk through every path described by its dependencies. Each time we visit a node we haven’t seen before, we walk through its dependencies as well. Only after visiting all of a node’s dependencies do we add it to a list that contains the sorted nodes.
The end result is that we find all of the leaf nodes first (those without any dependencies) and add those to the list initially. After that, the nodes that depend on the leaf nodes get added to the list, then the ones that depend on those, etc., until we have added all the nodes to the list. As we visit leaf nodes first and work our way back from there, this is a depth-first search.
Let’s apply this to our example:
- A –> {B, C}
- B –> {}
- C –> {B}
| A | | | First visit – visit dependencies | |
| | B | | First visit – no dependencies to visit | Add B to list |
| | C | | First visit – visit dependencies | |
| | | B | Already visited | Add C to list |
| | | | | Add A to list |
| B | | | Already visited | |
| C | | | Already visited | |
After the algorithm runs, the list contains the nodes B, C, and A, as expected.
Detecting Cycles
A cycle is a set of nodes which are all interdependent:
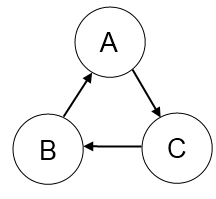
There is no valid topological sort for a graph with even a single cycle. The reason is clear: where would we start, and where would we end? This is a form of an infinite loop which would be useful to detect. Grasp should make it easy to find and fix calculation cycles.
We can modify the topological sort to encompass this new requirement. The trick is to keep track of every set of nodes visited in the context of a root node; if we see the same node twice, we have identified a cycle. (A root node is one which we are visiting on its own, outside the context of any other node. In the example above, the leftmost column contains the root nodes.)
Let’s apply this to our circular example:
| A | | | | First visit – visit dependencies |
| | C | | | First visit – visit dependencies |
| | | B | | First visit – visit dependencies |
| | | | A | Already visited in context of A – cycle detected |
When we see A again, we know that some part of the graph is cyclical. We stop sorting nodes and raise an error containing the repeated node and all those above it. This gives schema designers plenty of debugging information.
Visit History
We have identified two pieces of context while sorting nodes:
- All nodes we have visited
- All nodes within the current root node
We can pair this data and logic via a class representing the visit history, nesting it privately within DependencyGraph:
private sealed class VisitHistory
{
private HashSet<DependencyNode> _visitedNodes = new HashSet<DependencyNode>();
private HashSet<DependencyNode> _visitedNodesFromRoot;
private List<DependencyNode> _visitedNodesFromRootInOrder;
internal void OnVisitingRootNode()
{
_visitedNodesFromRoot = new HashSet<DependencyNode>();
_visitedNodesFromRootInOrder = new List<DependencyNode>();
}
internal bool OnVisitingNode(DependencyNode node)
{
if(_visitedNodesFromRoot.Contains(node))
{
throw new CalculationCycleException(_visitedNodesFromRootInOrder, node);
}
var firstVisit = !_visitedNodes.Contains(node);
if(firstVisit)
{
_visitedNodes.Add(node);
_visitedNodesFromRoot.Add(node);
_visitedNodesFromRootInOrder.Add(node);
}
return firstVisit;
}
}
The first method signals we are starting a visit of a root node. We create a new set to track the nodes we visit underneath it.
The second method signals that we are visiting some node in the graph. The first thing we do is check whether we have visited the same node in the context of the current root node; if so, we have detected a cycle and stop the sort by throwing an exception.
After that, we determine if we have seen the node before. If not, we track in the overall visited node set as well as the set of nodes under the current root node. We also keep an ordered list so we can provide the exact cycle sequence (sets have an undefined order). Finally, we return whether this is the first visit, since we will use that to determine whether we visit the node’s dependencies.
Algorithm
The TopologicalSort class is also private to the DependencyGraph class. It exposes the SortNodes method we used to implement the DependencyGraph.OrderCalculations method above:
private sealed class TopologicalSort
{
private readonly VisitHistory _visitHistory = new VisitHistory();
private readonly List<DependencyNode> _sortedNodes = new List<DependencyNode>();
private readonly DependencyGraph _graph;
internal TopologicalSort(DependencyGraph graph)
{
_graph = graph;
}
internal IEnumerable<DependencyNode> SortNodes()
{
foreach(var rootNode in _graph.GetNodes())
{
_visitHistory.OnVisitingRootNode();
VisitNode(rootNode);
}
return _sortedNodes;
}
private void VisitNode(DependencyNode node)
{
var firstVisit = _visitHistory.OnVisitingNode(node);
if(firstVisit)
{
foreach(var dependencyNode in _graph.GetDependencyNodes(node))
{
VisitNode(dependencyNode);
}
_sortedNodes.Add(node);
}
}
}
We create a visit history to track visits during the sort, and a list to contain the sorted nodes. The SortNodes method implements the algorithm we described above: it iterates through all of the nodes in the graph, signals the history for each of them, and visits them. It simply returns the list of sorted nodes when done.
The VisitNode method is the workhorse. It first signals to the history that it is visiting a node; it receives in response a flag indicating whether the node is being visited for the first time. If so, it gets the nodes for each of the current node’s dependencies and visits those as well. Only after all of the dependencies are visited does it add the current node to the list of sorted nodes. This recursion implements the depth-first search as described earlier.
TopologicalSort uses two methods we haven’t yet defined on DependencyGraph: GetNodes and GetDependencyNodes. These are fairly straightforward:
private IEnumerable<DependencyNode> GetNodes()
{
return _nodes.Values;
}
private IEnumerable<DependencyNode> GetDependencyNodes(DependencyNode node)
{
return node.Dependencies.Select(dependency => _nodes[dependency]);
}
GetNodes gets all of the values in the calculation->node dictionary. GetDependencyNodes translates the values in the Dependencies property, which are calculations, into the nodes associated with those calculations.
Summary
We identified a data structure that can represent dependencies between calculations: the graph. We turned a set of calculations into a set of nodes and sorted them according to the well-known topological sort algorithm. We also detected cycles and reported all relevant information so Grasp users can debug their schemas. We ultimately produced the compiled calculations, in order of dependency, that GraspRuntime applies to a set of variables.
That’s it! We have seen everything that goes into defining, compiling, and executing a set of calculations on a data set. This is the starting point for a family of application types which otherwise require lots of custom code; it frees developers to worry about business problems instead of the mechanics of analysis.
I plan on putting the entire codebase on GitHub and posting the URI soon. I also want to create some usage examples and discuss future possibilities (an example: frame a UI as a set of variables, validation rules as a set of boolean-valued calculations, and Grasp would do nicely at the core of a widely-applicable validation system.)
It promises to be a fun ride. And if you have read this far, thanks for indulging me!


 Posts
Posts